O Que É Ordem De Grandeza Exemplos nos apresenta um conceito fundamental que auxilia na compreensão e estimativa de quantidades em diversos aspectos da vida. Este conceito nos permite lidar com dados complexos e tomar decisões informadas em meio à incerteza.
Ao longo deste artigo, exploraremos o significado da ordem de grandeza, métodos para estimá-la e suas aplicações práticas. Além disso, forneceremos exemplos concretos e uma tabela abrangente para ilustrar sua utilidade em vários cenários.
O que é Ordem de Grandeza?: O Que É Ordem De Grandeza Exemplos
Ordem de grandeza é um conceito matemático que descreve a magnitude aproximada de um número ou quantidade. Ele fornece uma maneira de comparar e classificar números com base em seus valores relativos, sem se preocupar com precisão exata.
Na vida cotidiana, usamos a ordem de grandeza para fazer estimativas rápidas e tomar decisões informadas. Por exemplo, podemos estimar a distância de uma cidade vizinha em centenas de quilômetros, mesmo sem saber a distância exata. Ou podemos estimar o número de pessoas em um estádio em milhares, sem contar cada indivíduo.
Usando Ordens de Grandeza, O Que É Ordem De Grandeza Exemplos
Existem várias maneiras de expressar a ordem de grandeza de um número:
- Notação científica:A notação científica é uma forma de representar números muito grandes ou muito pequenos usando potências de 10. Por exemplo, o número 602.214.129.000.000.000.000.000 pode ser escrito como 6,02214129 x 10^23.
- Prefixos do SI:Os prefixos do SI são um conjunto de prefixos usados para representar potências de 10. Por exemplo, o prefixo “quilo” representa 10^3, então 1 quilograma é igual a 1.000 gramas.
- Ordens de magnitude:Podemos simplesmente dizer que um número está na ordem de grandeza de 10, 100, 1.000 e assim por diante. Por exemplo, a população da Terra é da ordem de grandeza de 10 bilhões.
Métodos para Estimar a Ordem de Grandeza

Para estimar a ordem de grandeza de uma quantidade, existem vários métodos disponíveis, cada um com suas vantagens e desvantagens. Os métodos mais comuns incluem:
A seguir, vamos explorar cada um desses métodos com mais detalhes:
Comparação com quantidades conhecidas
Este método envolve comparar a quantidade em questão com quantidades conhecidas cuja ordem de grandeza é conhecida. Por exemplo, se você quiser estimar a ordem de grandeza da população da Terra, você pode compará-la com a população de sua cidade ou país, cuja ordem de grandeza você já conhece.
Análise dimensional
Este método usa as unidades da quantidade para determinar sua ordem de grandeza. Por exemplo, se você quiser estimar a ordem de grandeza da velocidade da luz, você sabe que sua unidade é metros por segundo. Como o metro é uma unidade de comprimento e o segundo é uma unidade de tempo, você pode concluir que a ordem de grandeza da velocidade da luz é metros por segundo.
Uso de aproximações
Este método envolve aproximar a quantidade por um valor mais simples cuja ordem de grandeza é conhecida. Por exemplo, se você quiser estimar a ordem de grandeza da raiz quadrada de 100, você pode aproximá-la por 10, cuja ordem de grandeza é 10 1.
Aplicações da Ordem de Grandeza
A ordem de grandeza é uma ferramenta poderosa que pode ser usada em uma ampla gama de aplicações. Algumas das aplicações mais importantes incluem:
Tomada de decisão rápida
A ordem de grandeza pode ser usada para tomar decisões rápidas em situações onde a precisão exata não é necessária. Por exemplo, um gerente de projeto pode usar a ordem de grandeza para estimar o custo de um novo projeto.
Isso pode ajudá-lo a decidir se o projeto é viável ou não, sem precisar gastar muito tempo em cálculos detalhados.
Resolução de problemas complexos
A ordem de grandeza também pode ser usada para resolver problemas complexos. Por exemplo, um cientista pode usar a ordem de grandeza para estimar a quantidade de energia necessária para aquecer um planeta. Isso pode ajudá-lo a desenvolver novas teorias sobre a evolução do sistema solar.
Estimativa de parâmetros desconhecidos
A ordem de grandeza pode ser usada para estimar parâmetros desconhecidos. Por exemplo, um engenheiro pode usar a ordem de grandeza para estimar a resistência de um novo material. Isso pode ajudá-lo a projetar estruturas mais seguras e eficientes.
Exemplos de Ordem de Grandeza
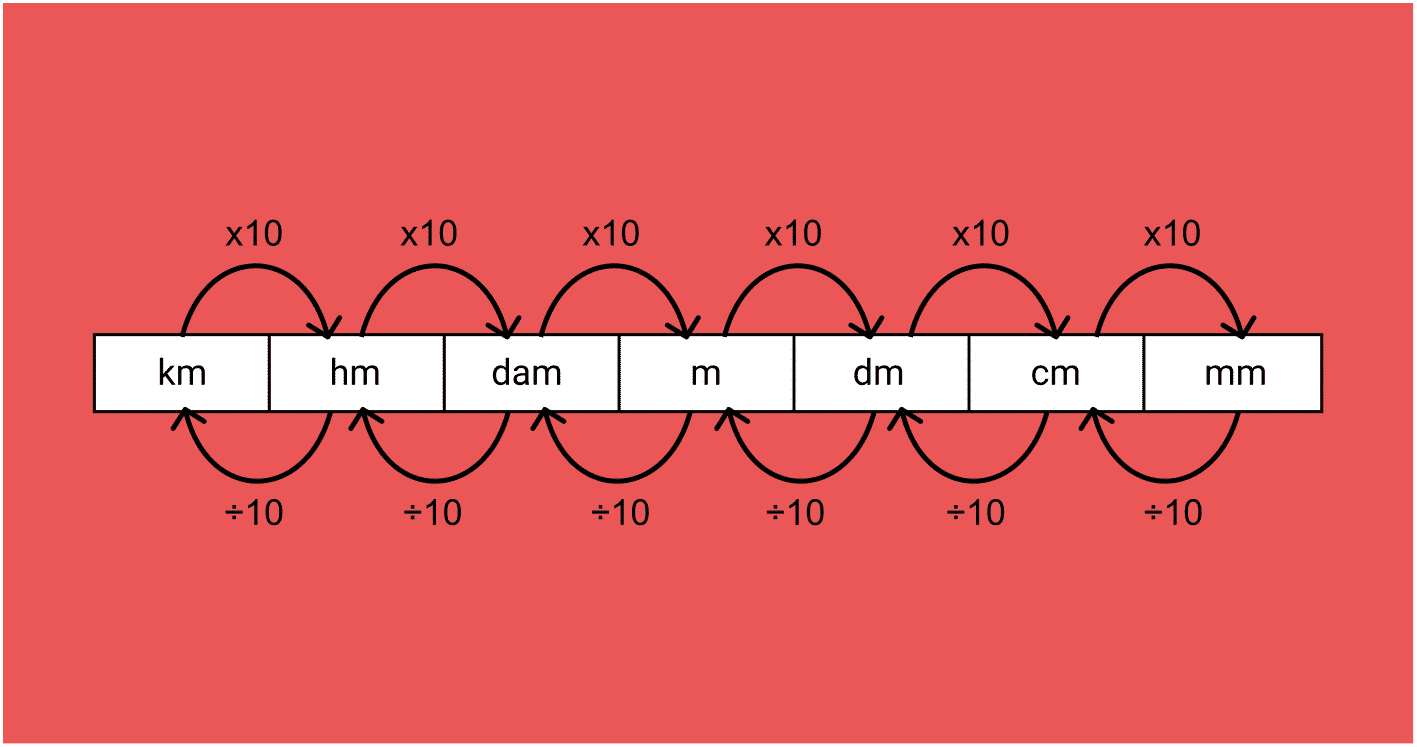
Os exemplos de ordem de grandeza fornecem estimativas úteis de quantidades que podem ser difíceis de medir ou calcular com precisão.
Aqui estão alguns exemplos comuns de ordem de grandeza:
População da Terra
- 10 bilhões (10 10)
Distância da Terra ao Sol
- 150 milhões de quilômetros (1,5 x 10 8km)
Número de estrelas na Via Láctea
- 100 bilhões (10 11)
Tabela de Exemplos de Ordem de Grandeza

A tabela a seguir apresenta uma lista de exemplos de ordens de grandeza, seus valores aproximados e uma breve descrição:
| Ordem de Grandeza | Valor Aproximado | Descrição |
|---|---|---|
| 10-30 | Tamanho de um átomo | O tamanho aproximado de um átomo é de 10-10 metros. |
| 10-15 | Tamanho de uma célula | O tamanho aproximado de uma célula é de 10-6 metros. |
| 10-3 | Tamanho de um ser humano | O tamanho aproximado de um ser humano é de 1 metro. |
| 103 | Tamanho da Terra | O diâmetro aproximado da Terra é de 12.742 quilômetros. |
| 106 | Tamanho do Sol | O diâmetro aproximado do Sol é de 1.392.000 quilômetros. |
| 1012 | Tamanho da Via Láctea | O diâmetro aproximado da Via Láctea é de 100.000 anos-luz. |
| 1024 | Tamanho do universo observável | O diâmetro aproximado do universo observável é de 93 bilhões de anos-luz. |
Em suma, a ordem de grandeza é uma ferramenta valiosa que nos permite quantificar e comparar quantidades em situações cotidianas e científicas. Ao compreender e aplicar esse conceito, podemos aprimorar nossa capacidade de resolver problemas, tomar decisões e entender o mundo ao nosso redor de forma mais precisa e significativa.
User Queries
O que é ordem de grandeza?
A ordem de grandeza refere-se à magnitude aproximada de uma quantidade, expressa como um expoente de 10.
Como estimar a ordem de grandeza?
Podemos estimar a ordem de grandeza por meio de comparação com quantidades conhecidas, análise dimensional ou uso de aproximações.
Quais são as aplicações da ordem de grandeza?
A ordem de grandeza é amplamente utilizada na tomada de decisão rápida, resolução de problemas complexos e estimativa de parâmetros desconhecidos.

