Exemplo De Sistema De NumeraçãO Decimal

Exemplo De Sistema De Numeração Decimal, a base do nosso sistema numérico, nos guia através de um universo de números e contagem. Desde a contagem de objetos simples até complexas operações matemáticas, o sistema decimal permeia todos os aspectos da nossa vida.

Neste artigo, iremos mergulhar no coração do sistema decimal, explorando seus conceitos fundamentais, suas aplicações e como ele molda nossa compreensão do mundo.

O sistema decimal, também conhecido como sistema de base dez, é o sistema de numeração que usamos diariamente. Sua base é dez, o que significa que utiliza dez dígitos (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) para representar todos os números.

Cada dígito possui um valor posicional, que determina seu peso dentro do número. Por exemplo, no número 234, o dígito 2 representa 200, o dígito 3 representa 30 e o dígito 4 representa 4. Essa estrutura permite que representemos números infinitamente grandes, desde os menores até os maiores.

Introdução ao Sistema Decimal: Exemplo De Sistema De Numeração Decimal

O sistema decimal, também conhecido como sistema de base 10, é o sistema de numeração mais comumente usado em todo o mundo. Ele é baseado em dez dígitos distintos (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) e utiliza o conceito de valor posicional para representar números.

Em contraste com outros sistemas de numeração, como o binário (base 2) e o hexadecimal (base 16), o sistema decimal utiliza dez símbolos distintos para representar os números. Essa base decimal, que representa o número de símbolos usados, é a razão pela qual o sistema é chamado de decimal.

O sistema decimal está presente em nossa vida cotidiana de várias maneiras. Usamos números decimais para contar dinheiro, medir distâncias, registrar tempo e muito mais. Ele é a base para a maioria dos cálculos matemáticos e é fundamental para a compreensão de conceitos científicos e tecnológicos.

Conceitos Fundamentais

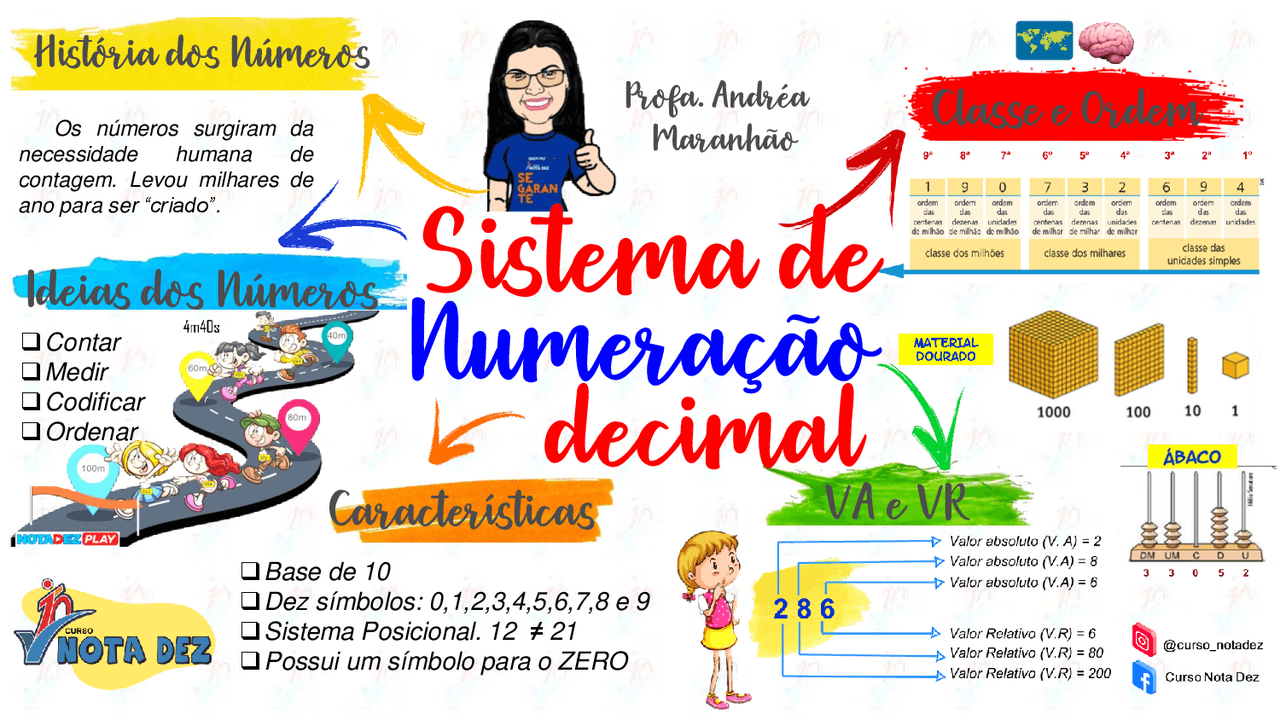
O sistema decimal é baseado em três conceitos fundamentais: dígitos, valor posicional e base.

• Dígitos:Os dez símbolos únicos (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) usados no sistema decimal são chamados de dígitos. Cada dígito representa um valor específico, de 0 a 9.
• Valor Posicional:O valor posicional de um dígito em um número decimal é determinado pela sua posição em relação à vírgula decimal. Cada posição representa uma potência de 10, começando da direita para a esquerda. Por exemplo, no número 123, o dígito 3 está na posição das unidades, o dígito 2 está na posição das dezenas e o dígito 1 está na posição das centenas.

• Base:A base do sistema decimal é 10, o que significa que existem dez dígitos distintos usados para representar números. Cada posição no número representa uma potência de 10, começando com 10⁰ (que é igual a 1) para a posição das unidades, 10¹ (que é igual a 10) para a posição das dezenas, 10² (que é igual a 100) para a posição das centenas, e assim por diante.

Operações Matemáticas no Sistema Decimal

O sistema decimal facilita a realização de operações matemáticas como adição, subtração, multiplicação e divisão. O conceito de valor posicional desempenha um papel crucial nesses cálculos.

• Adição:Para adicionar números decimais, os dígitos de cada posição são somados individualmente, levando em consideração os “carries” (vai um) quando a soma excede 9. Por exemplo, para adicionar 123 + 456, somamos os dígitos das unidades (3 + 6 = 9), os dígitos das dezenas (2 + 5 = 7) e os dígitos das centenas (1 + 4 = 5), resultando em 579.

• Subtração:A subtração de números decimais é semelhante à adição, mas envolve “emprestar” (toma um) de posições adjacentes quando um dígito é menor que o dígito correspondente no minuendo. Por exemplo, para subtrair 321 de 543, subtraímos os dígitos das unidades (3 – 1 = 2), os dígitos das dezenas (4 – 2 = 2) e os dígitos das centenas (5 – 3 = 2), resultando em 222.

• Multiplicação:A multiplicação de números decimais envolve multiplicar cada dígito do multiplicando por cada dígito do multiplicador, somando os resultados parciais, levando em consideração o valor posicional de cada dígito. Por exemplo, para multiplicar 123 por 456, multiplicamos cada dígito de 123 por 456, adicionando os resultados parciais, levando em consideração o valor posicional de cada dígito.

• Divisão:A divisão de números decimais envolve dividir o dividendo pelo divisor, usando o conceito de valor posicional para determinar o quociente e o resto. Por exemplo, para dividir 123 por 4, dividimos o dividendo 123 pelo divisor 4, resultando em um quociente de 30 e um resto de 3.

Conversão de Números

O sistema decimal pode ser usado para converter números de outros sistemas de numeração, como binário, hexadecimal e romano, para o sistema decimal.

• Binário para Decimal:Para converter um número binário para decimal, cada dígito binário é multiplicado por uma potência de 2, começando da direita para a esquerda, com a primeira posição representando 2⁰, a segunda posição representando 2¹, a terceira posição representando 2², e assim por diante.

  Os resultados são somados para obter o equivalente decimal. Por exemplo, o número binário 1011 é convertido para decimal da seguinte forma: (1 x 2³) + (0 x 2²) + (1 x 2¹) + (1 x 2⁰) = 8 + 0 + 2 + 1 = 11.

• Hexadecimal para Decimal:Para converter um número hexadecimal para decimal, cada dígito hexadecimal é multiplicado por uma potência de 16, começando da direita para a esquerda, com a primeira posição representando 16⁰, a segunda posição representando 16¹, a terceira posição representando 16², e assim por diante.

  Os resultados são somados para obter o equivalente decimal. Por exemplo, o número hexadecimal A3 é convertido para decimal da seguinte forma: (10 x 16¹) + (3 x 16⁰) = 160 + 3 = 163.

• Romano para Decimal:Para converter um número romano para decimal, cada símbolo romano é substituído pelo seu valor decimal correspondente. Os valores são somados se o símbolo da esquerda for menor ou igual ao símbolo da direita. Caso contrário, o valor do símbolo da esquerda é subtraído do valor do símbolo da direita.

  Por exemplo, o número romano MCMXCIX é convertido para decimal da seguinte forma: (1000 – 100) + (1000 – 10) + (10 – 1) = 1999.

Aplicações do Sistema Decimal

O sistema decimal desempenha um papel crucial na ciência, tecnologia e vida cotidiana. Sua importância reside em sua simplicidade, flexibilidade e capacidade de representar números de forma eficiente.

• Matemática:O sistema decimal é a base para a maioria dos cálculos matemáticos, incluindo operações aritméticas, álgebra, geometria e cálculo. Ele fornece um sistema consistente para representar números e realizar operações matemáticas complexas.
• Computação:Embora os computadores usem o sistema binário, o sistema decimal é usado para interagir com os computadores e interpretar dados. Ele é usado em interfaces de usuário, sistemas operacionais e programas de software para representar números e realizar cálculos.
• Finanças:O sistema decimal é usado em transações financeiras, incluindo dinheiro, taxas de juros, investimentos e contabilidade. Ele fornece uma base comum para representar valores monetários e realizar cálculos financeiros.
• Comércio:O sistema decimal é usado em comércio para registrar preços, quantidades, estoques e transações. Ele fornece um sistema consistente para realizar cálculos comerciais e gerenciar estoque.

Commonly Asked Questions

Por que o sistema decimal é tão importante?

O sistema decimal é a base do nosso sistema numérico e é usado em todo o mundo para contagem, cálculos e representação de quantidades. Sua simplicidade e flexibilidade o tornam ideal para uma ampla gama de aplicações.

Quais são as vantagens do sistema decimal?

O sistema decimal é intuitivo, fácil de aprender e usar. Sua base dez permite representar números de forma eficiente, utilizando apenas dez dígitos. Além disso, a estrutura posicional facilita a realização de operações matemáticas.

Existem outros sistemas de numeração além do decimal?

Sim, existem outros sistemas de numeração, como o binário (base dois), o hexadecimal (base dezesseis) e o romano. Cada sistema possui suas próprias características e aplicações específicas.