Exemplo De Funções E Representação De Graficos De Função Exponencial é um tema fundamental no estudo de matemática, abrangendo conceitos que permeiam diversas áreas do conhecimento. Mergulhando neste universo, exploraremos as características e propriedades das funções exponenciais, desvendando sua aplicação em cenários reais e compreendendo como sua representação gráfica fornece insights valiosos para a análise de fenômenos complexos.
Este guia aborda a definição de funções exponenciais, sua forma geral e propriedades essenciais. Através de exemplos práticos, como crescimento populacional e decaimento radioativo, demonstraremos como as funções exponenciais modelam fenômenos do mundo real. Abordaremos a representação gráfica dessas funções, detalhando os passos para construir o gráfico e interpretar suas características, como crescimento, decrescimento, domínio e imagem.
Introdução às Funções Exponenciais: Exemplo De Funções E Representação De Graficos De Função Exponencial
As funções exponenciais são um tipo fundamental de função matemática que desempenha um papel crucial em diversas áreas, incluindo matemática, ciência, engenharia e finanças. Essas funções caracterizam-se por seu crescimento ou decrescimento rápido, que as torna ferramentas essenciais para modelar fenômenos que envolvem taxas de mudança exponenciais.
A forma geral de uma função exponencial é dada por:
f(x) = a^x
onde a é a base da função, um número real diferente de zero e 1, e x é o expoente, uma variável real.
Propriedades Básicas
As funções exponenciais possuem propriedades importantes que as distinguem de outros tipos de funções. Essas propriedades determinam seu comportamento e permitem a análise de seus gráficos:
- Crescimento ou Decrescimento:Se a base a for maior que 1, a função é crescente, ou seja, seu valor aumenta à medida que x aumenta. Se a base a estiver entre 0 e 1, a função é decrescente, ou seja, seu valor diminui à medida que x aumenta.
- Domínio:O domínio de uma função exponencial é o conjunto de todos os números reais. Isso significa que a função está definida para qualquer valor de x.
- Imagem:A imagem de uma função exponencial é o conjunto de todos os números reais positivos, se a base a for maior que 1. Se a base a estiver entre 0 e 1, a imagem é o conjunto de todos os números reais positivos, exceto 0.
Exemplos de Funções Exponenciais
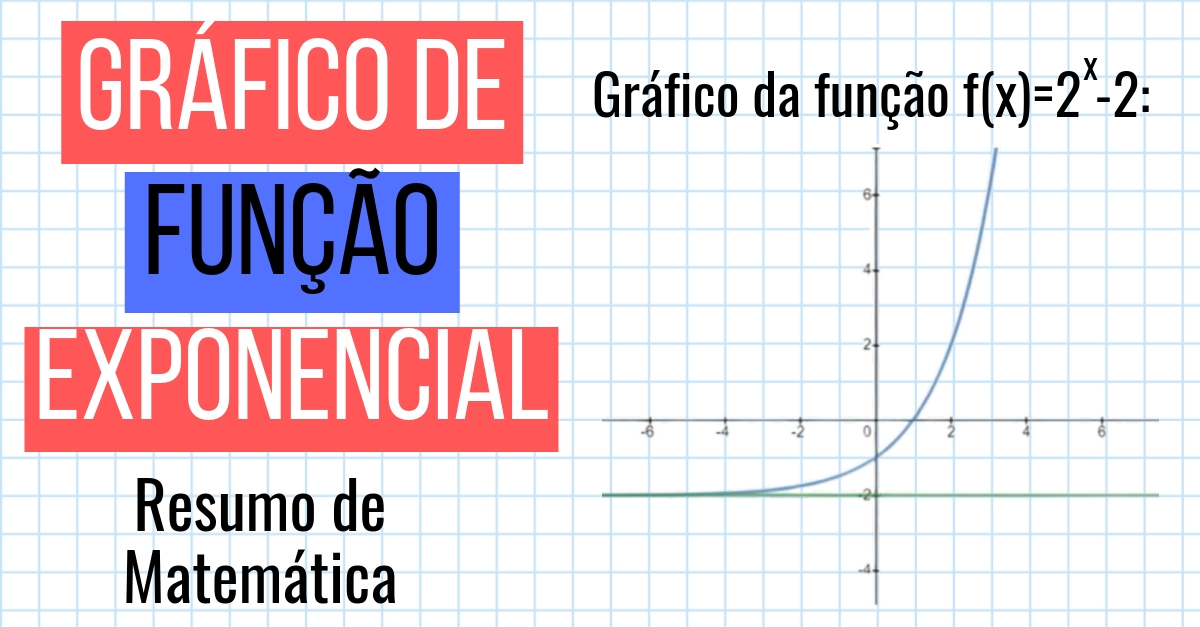
As funções exponenciais aparecem em diversos contextos da vida real, modelando fenômenos que se desenvolvem de forma exponencial. Alguns exemplos incluem:
Tabela de Exemplos
| Contexto | Equação da Função | Descrição |
|---|---|---|
| Crescimento Populacional | P(t) = P0
|
Modela o crescimento populacional de uma determinada região, onde P(t) é a população no tempo t, P0é a população inicial, r é a taxa de crescimento e e é a constante de Euler. |
| Decaimento Radioativo | N(t) = N0
|
Modela a quantidade de um material radioativo que decai ao longo do tempo, onde N(t) é a quantidade no tempo t, N0é a quantidade inicial, λ é a constante de decaimento e e é a constante de Euler. |
| Juros Compostos | A(t) = P
|
Modela o valor de um investimento que rende juros compostos, onde A(t) é o valor no tempo t, P é o principal, r é a taxa de juros, n é o número de vezes que os juros são compostos por ano e t é o tempo em anos. |
Representação Gráfica de Funções Exponenciais
O gráfico de uma função exponencial é uma curva característica que se estende para cima ou para baixo, dependendo da base da função. Para construir o gráfico de uma função exponencial, podemos seguir os seguintes passos:
- Escolha de Pontos:Selecione alguns valores para x e calcule os valores correspondentes de f(x) usando a equação da função.
- Identificação de Intersecções com os Eixos:Encontre os pontos onde o gráfico intercepta os eixos x e y. A intersecção com o eixo y ocorre em x = 0, e a intersecção com o eixo x ocorre quando f(x) = 0, se existir.
- Análise do Comportamento da Função:Observe o comportamento da função para valores grandes e pequenos de x. Se a base a for maior que 1, o gráfico se estenderá para cima à medida que x aumenta. Se a base a estiver entre 0 e 1, o gráfico se estenderá para baixo à medida que x aumenta.
Por exemplo, o gráfico da função exponencial f(x) = 2 xé uma curva que se estende para cima à medida que x aumenta. A intersecção com o eixo y ocorre em (0, 1), e o gráfico não intercepta o eixo x.
A função é crescente e seu domínio é o conjunto de todos os números reais, enquanto sua imagem é o conjunto de todos os números reais positivos.
Análise de Gráficos de Funções Exponenciais
Ao analisar um gráfico de uma função exponencial, podemos extrair informações importantes sobre a função, como sua base, seu crescimento ou decrescimento, seu domínio e sua imagem.
- Base:A base da função pode ser determinada observando a inclinação do gráfico. Se o gráfico estiver subindo à medida que x aumenta, a base é maior que 1. Se o gráfico estiver descendo à medida que x aumenta, a base está entre 0 e 1.
- Crescimento ou Decrescimento:O comportamento da função, se crescente ou decrescente, pode ser observado pela inclinação do gráfico. Se o gráfico estiver subindo, a função é crescente. Se o gráfico estiver descendo, a função é decrescente.
- Domínio e Imagem:O domínio da função é o conjunto de todos os valores de x para os quais a função está definida. A imagem da função é o conjunto de todos os valores de f(x) que a função pode assumir.
Aplicações de Funções Exponenciais
As funções exponenciais têm aplicações em diversas áreas, incluindo:
- Finanças:As funções exponenciais são usadas para modelar o crescimento de investimentos, juros compostos e o valor do dinheiro ao longo do tempo.
- Medicina:As funções exponenciais são usadas para modelar o crescimento de bactérias, a propagação de doenças e a eliminação de medicamentos do corpo.
- Engenharia:As funções exponenciais são usadas para modelar o decaimento radioativo, a transferência de calor e o comportamento de circuitos elétricos.
- Ciência da Computação:As funções exponenciais são usadas para modelar o crescimento de algoritmos, o desempenho de redes e a complexidade de problemas computacionais.
Em resumo, as funções exponenciais são ferramentas matemáticas poderosas que desempenham um papel fundamental em diversos campos. Seu crescimento ou decrescimento rápido e suas propriedades únicas as tornam essenciais para modelar e analisar fenômenos que envolvem taxas de mudança exponenciais.

