Introdução ao Cálculo do Núcleo e da Imagem de Transformações Lineares: Exemplo De Cálculo Do Nucleo E Imagem De Transformacoes Lineares

Exemplo De Cálculo Do Nucleo E Imagem De Transformacoes Lineares – O estudo do núcleo e da imagem de uma transformação linear é fundamental para a compreensão completa de suas propriedades e comportamento. Estas estruturas fornecem insights cruciais sobre como a transformação afeta os vetores do espaço vetorial de origem. Dominar o cálculo do núcleo e da imagem permite a análise de propriedades importantes da transformação, como injetividade e sobrejetividade, e sua representação geométrica.
Definição Formal de Núcleo e Imagem
O núcleo (ou kernel) de uma transformação linear T: V → W, denotado por Ker(T), é o subespaço vetorial de V formado por todos os vetores v em V tais que T(v) = 0 (o vetor nulo em W). A imagem de T, denotada por Im(T), é o subespaço vetorial de W formado por todos os vetores w em W para os quais existe um vetor v em V tal que T(v) = w.
Em outras palavras, o núcleo contém todos os vetores que são “mapeados” para o vetor nulo, enquanto a imagem contém todos os vetores que são “atingidos” pela transformação. A relação entre o núcleo, a imagem e o domínio é que o domínio é o espaço vetorial V de onde a transformação parte, o núcleo é um subespaço vetorial do domínio, e a imagem é um subespaço vetorial do contradomínio W.
O cálculo do núcleo e da imagem é crucial para determinar a injetividade (núcleo trivial) e sobrejetividade (imagem igual ao contradomínio) da transformação.
Métodos para o Cálculo do Núcleo
O cálculo do núcleo de uma transformação linear, frequentemente representada por uma matriz A, envolve a resolução de um sistema de equações lineares homogêneo Ax = 0. Este processo identifica os vetores que são mapeados para o vetor nulo pela transformação.
- Primeiramente, monta-se a matriz aumentada [A|0], onde 0 representa a matriz coluna de zeros.
- Em seguida, aplica-se o método de eliminação de Gauss-Jordan para reduzir a matriz aumentada à sua forma escalonada reduzida por linhas.
- As variáveis correspondentes às colunas sem pivô (colunas sem 1 na forma escalonada reduzida) são as variáveis livres, que podem ser parametrizadas para expressar o núcleo como combinação linear de vetores linearmente independentes.
- Por fim, esses vetores linearmente independentes formam uma base para o núcleo.
A base do núcleo pode ser encontrada através de diferentes métodos, como a redução de linhas ou o uso de decomposições matriciais (como a decomposição em valores singulares). A escolha do método depende da complexidade da matriz e das ferramentas disponíveis.
| Matriz A | Forma Escalonada Reduzida | Variáveis Livres | Base do Núcleo |
|---|---|---|---|
[[1, 2], [3, 6]] |
[[1, 2], [0, 0]] |
x2 |
[-2, 1] |
[[1, 0, 1], [0, 1, 0]] |
[[1, 0, 1], [0, 1, 0]] |
x3 |
[-1, 0, 1] |
[[1, 2, 3], [4, 5, 6], [7, 8, 9]] |
[[1, 0, -1], [0, 1, 2], [0, 0, 0]] |
x3 |
[1, -2, 1] |
[[0, 0], [0, 0]] |
[[0, 0], [0, 0]] |
x1, x 2 |
[1, 0], [0, 1] |
Métodos para o Cálculo da Imagem
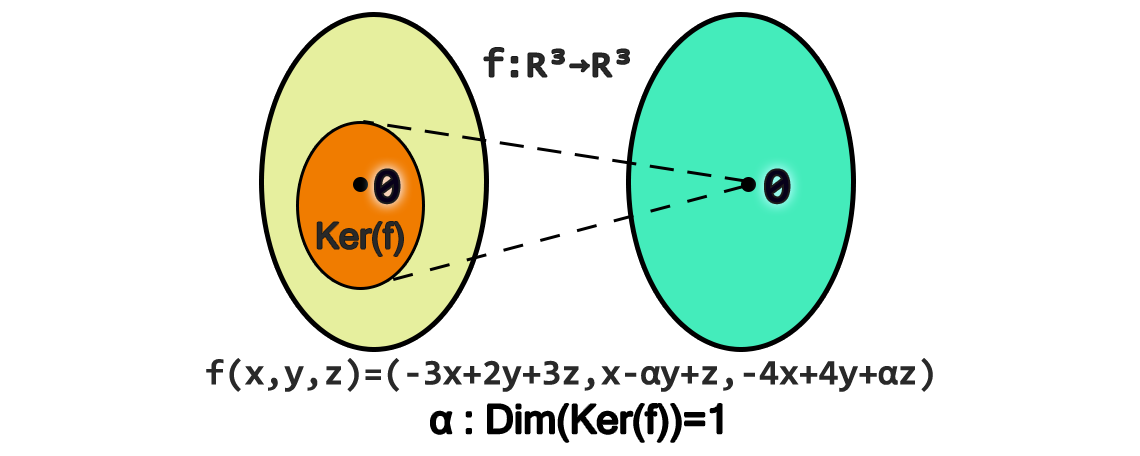
A imagem de uma transformação linear representada por uma matriz A é o espaço vetorial gerado pelas colunas de A. Para calcular a imagem, podemos utilizar a redução de linhas para encontrar uma base para o espaço coluna.
O processo envolve aplicar operações elementares de linha na matriz A até obter sua forma escalonada reduzida por linhas. As colunas da matriz original correspondentes às colunas pivô (colunas com 1 na forma escalonada reduzida) formam uma base para a imagem. A dimensão da imagem, também conhecida como posto da matriz, é igual ao número de colunas pivô.
Exemplos Práticos de Cálculo
Vamos calcular o núcleo e a imagem de uma transformação linear representada pela matriz A = [[1, 2, 3], [4, 5, 6]]. Para o núcleo, resolvemos Ax = 0. Após a redução de linhas, obtemos a forma escalonada reduzida e determinamos a base do núcleo. Para a imagem, as colunas pivôs da forma escalonada reduzida indicam a base da imagem.
Um exemplo com uma matriz 3×2 segue um procedimento análogo, mas a interpretação geométrica pode ser mais complexa em dimensões superiores. A transformação linear T(x, y) = (x + y, x – y) mapeia o plano em si mesmo. O núcleo é o ponto (0,0) e a imagem é todo o R².
| Matriz | Núcleo | Imagem | Dimensão da Imagem |
|---|---|---|---|
| [[1, 2, 3], [4, 5, 6]] | (espaço vetorial gerado por um vetor, encontrado através da resolução do sistema linear homogêneo) | (espaço vetorial gerado por duas colunas linearmente independentes da matriz) | 2 |
| [[1, 2], [3, 4], [5, 6]] | (vetor nulo) | (espaço vetorial gerado por duas colunas linearmente independentes da matriz) | 2 |
Representação Geométrica do Núcleo e da Imagem, Exemplo De Cálculo Do Nucleo E Imagem De Transformacoes Lineares
Geometricamente, o núcleo representa o conjunto de vetores que são mapeados para o vetor nulo pela transformação. Em R², pode ser um ponto (transformação injetiva), uma reta que passa pela origem, ou todo o espaço (transformação nula). A imagem representa o subespaço vetorial gerado pelos vetores transformados. Em R², pode ser um ponto, uma reta, ou todo o espaço.
Em transformações lineares em R², o núcleo pode ser visualizado como uma reta ou um ponto, enquanto a imagem pode ser uma reta ou todo o plano.
Em R³, o núcleo pode ser um ponto, uma reta, um plano, ou todo o espaço, enquanto a imagem pode ser um ponto, uma reta, um plano, ou todo o espaço.
Teorema do Núcleo e da Imagem
O Teorema do Núcleo e da Imagem afirma que, para uma transformação linear T: V → W, a dimensão do domínio V é igual à soma da dimensão do núcleo e da dimensão da imagem: dim(V) = dim(Ker(T)) + dim(Im(T)). Este teorema estabelece uma relação fundamental entre as dimensões do núcleo e da imagem, mostrando como a transformação “distribui” a dimensão do domínio entre essas duas estruturas.
A aplicação deste teorema em exemplos concretos permite a verificação e a compreensão de suas implicações na análise de transformações lineares.
Ao concluir nossa exploração do cálculo do núcleo e da imagem de transformações lineares, fica evidente a importância desses conceitos para a compreensão profunda da álgebra linear. Dominar esses métodos não se limita à resolução de exercícios acadêmicos; abre portas para a solução de problemas em áreas como processamento de imagens, aprendizado de máquina e modelagem matemática em geral.
A capacidade de visualizar geometricamente o núcleo e a imagem enriquece a intuição e facilita a resolução de problemas mais complexos. Portanto, a jornada de aprendizado aqui apresentada é um investimento valioso para qualquer profissional ou estudante que busca excelência em matemática.

