Calculando Determinantes 3×3: Uma Abordagem Prática com a Regra de Sarrus: Determinante De 3 Ordem Com Regra De Sarrus E Exemplos
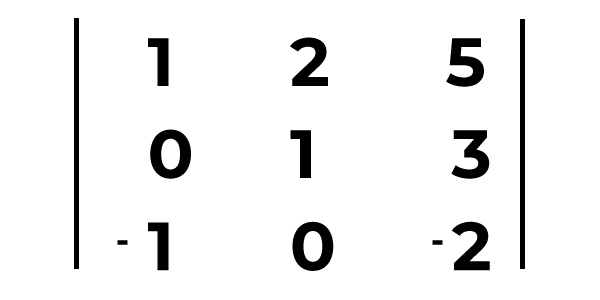
Determinante De 3 Ordem Com Regra De Sarrus E Exemplos – Determinar o determinante de uma matriz é uma operação fundamental em álgebra linear, com aplicações em diversas áreas, como geometria analítica, física e engenharia. Para matrizes 3×3, a Regra de Sarrus oferece um método eficiente e memorizável para calcular esse determinante. Este artigo irá explorar a Regra de Sarrus passo a passo, apresentando exemplos práticos, discutindo suas limitações e explorando suas aplicações em diferentes contextos.
Introdução à Regra de Sarrus

A Regra de Sarrus é um método prático para calcular o determinante de uma matriz quadrada de ordem 3. Ela simplifica o processo em comparação com a expansão de cofatores, tornando o cálculo mais rápido e intuitivo. O método envolve a repetição das duas primeiras colunas da matriz à direita, formando um diagrama que facilita a identificação dos produtos a serem somados e subtraídos.
Para uma matriz 3×3 da forma:
| a b c | | d e f | | g h i |
O determinante é calculado da seguinte maneira:
1. Repita as duas primeiras colunas à direita da matriz:
| a b c | a b | | d e f | d e | | g h i | g h |
2. Calcule os produtos das diagonais principais (de cima para baixo): a*e*i, b*f*g, c*d*h
3. Calcule os produtos das diagonais secundárias (de baixo para cima): g*e*c, h*f*a, i*d*b
4. Subtraia a soma dos produtos das diagonais secundárias da soma dos produtos das diagonais principais: Determinante = (a*e*i + b*f*g + c*d*h)
-(g*e*c + h*f*a + i*d*b)
A Regra de Sarrus não é diretamente comparável a outros métodos para matrizes 3×3, como a expansão de cofatores, pois ela oferece uma abordagem mais direta e visual. A expansão de cofatores, embora aplicável a matrizes de qualquer ordem, pode se tornar mais complexa para matrizes maiores que 3×3.
Exemplos Práticos da Regra de Sarrus
Vamos ilustrar a Regra de Sarrus com três exemplos, demonstrando matrizes com determinantes positivo, negativo e zero.
| Matriz | Cálculo passo-a-passo | Resultado | Observações |
|---|---|---|---|
| 1 2 3 |
| 4 5 6 |
| 7 8 9 |
|
(1*5*9 + 2*6*7 + 3*4*8) -(7*5*3 + 8*6*1 + 9*4*2) = (45 + 84 + 96) -(105 + 48 + 72) = 225 – 225 = 0 |
0 | O determinante é zero, indicando que as linhas (ou colunas) da matriz são linearmente dependentes. |
| 2 1 0 |
| 3 2 1 |
| 1 0 1 |
|
(2*2*1 + 1*1*1 + 0*3*0) -(1*2*0 + 0*1*2 + 1*3*1) = (4 + 1 + 0) -(0 + 0 + 3) = 5 – 3 = 2 |
2 | Determinante positivo. |
| 1 0 2 |
| 0 1 0 |
| 2 0 1 |
|
(1*1*1 + 0*0*2 + 2*0*0) -(2*1*2 + 0*0*1 + 1*0*0) = (1 + 0 + 0) -(4 + 0 + 0) = 1 – 4 = -3 |
-3 | Determinante negativo. |
Matrizes Especiais e a Regra de Sarrus, Determinante De 3 Ordem Com Regra De Sarrus E Exemplos
A Regra de Sarrus se comporta de maneira previsível em matrizes com características especiais.
Por exemplo, se uma linha ou coluna de uma matriz 3×3 for composta inteiramente de zeros, o determinante será zero. Isso ocorre porque todos os termos na expansão da Regra de Sarrus conterão um zero, resultando em um determinante nulo.
Trocar duas linhas ou colunas de uma matriz 3×3 muda o sinal do determinante. Observe os exemplos abaixo:
| Matriz Original | Determinante | Matriz com Linhas Trocadas | Determinante |
|---|---|---|---|
| 1 2 3 |
| 4 5 6 |
| 7 8 9 |
|
0 |
| 4 5 6 |
| 1 2 3 |
| 7 8 9 |
|
0 |
| 2 1 0 |
| 3 2 1 |
| 1 0 1 |
|
2 |
| 3 2 1 |
| 2 1 0 |
| 1 0 1 |
|
-2 |
A Regra de Sarrus simplifica o cálculo do determinante quando a matriz possui muitos zeros, pois reduz o número de operações necessárias.
Aplicações da Regra de Sarrus
A Regra de Sarrus encontra aplicações práticas em diversas áreas. Na geometria analítica, pode ser utilizada para calcular a área de um triângulo. Dados os vértices (x1, y1), (x2, y2), e (x3, y3), a área A é dada por:
A = (1/2)
|(x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2))|
Essa fórmula pode ser representada como o determinante de uma matriz 3×3:
A = (1/2)
|det([[x1, y1, 1], [x2, y2, 1], [x3, y3, 1]])|
Em física e engenharia, determinantes 3×3 são usados em problemas envolvendo vetores e matrizes, como o cálculo do produto vetorial entre dois vetores. Por exemplo, em mecânica, o momento de uma força em relação a um ponto pode ser calculado usando o produto vetorial.
Em sistemas de equações lineares, a regra de Cramer utiliza determinantes para encontrar as soluções. Para um sistema de três equações lineares com três incógnitas, a solução para cada incógnita pode ser expressa como a razão de dois determinantes.
Limitações da Regra de Sarrus
A principal limitação da Regra de Sarrus é sua aplicabilidade apenas a matrizes 3×3. Para matrizes de ordem superior, outros métodos, como a expansão de cofatores ou o método de eliminação de Gauss, são necessários. A complexidade computacional da Regra de Sarrus cresce cubicamente com o tamanho da matriz, tornando-a ineficiente para matrizes maiores.
Comparada com a expansão de cofatores para matrizes 3×3, a Regra de Sarrus geralmente é mais eficiente em termos de tempo de cálculo, pois requer menos operações aritméticas. No entanto, para matrizes de ordem superior, métodos como a decomposição LU ou a eliminação de Gauss são significativamente mais eficientes.
Para calcular determinantes de matrizes de ordem superior a 3, métodos como a expansão de cofatores, a fatoração LU, ou métodos numéricos iterativos são empregados, dependendo da dimensão da matriz e das características específicas do problema.
Posso usar a Regra de Sarrus em matrizes 4×4?
Não, brother. A Regra de Sarrus só funciona para matrizes 3×3. Para matrizes maiores, precisa de outros métodos, tipo Laplace ou o método de eliminação de Gauss.
E se a matriz tiver uma linha ou coluna com todos os elementos iguais a zero?
Moleza! O determinante vai ser zero, independente do resto da matriz. É só relaxar e anotar o zero.
Qual a utilidade disso tudo na vida real?
Aí, meu consagrado! Serve pra resolver sistemas de equações lineares, calcular áreas de triângulos, e até em física e engenharia, em problemas mais complexos. É tipo um superpoder matemático, saca?

